Problems
Table summarizing some features we want to test. To be refined or extended.
| Features | Pb 1 | Pb 2 | Pb 3 | Pb 4 | Pb 5 | Pb6 | Discussed in |
|---|---|---|---|---|---|---|---|
| blocking objects | X | X | bench. sugg. 3 | ||||
| large task spaces | X | X | bench. sugg. 3, diff. pb. inst. | ||||
| infeasible task operators | x | X | bench. sugg. 3, diff. pb. inst. | ||||
| trade-off motion planning/task planning | X | diff. pb. inst. | |||||
| non-monotonicity | X | X | bench. sugg. 4 | ||||
| NAMO | ? | X | X | X | Sidd. comment 4 | ||
| Non-geometric actions | X | Sidd. comment 4 |
Contents
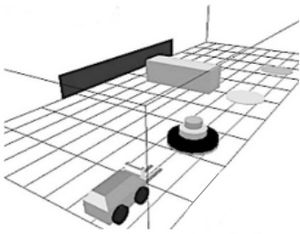
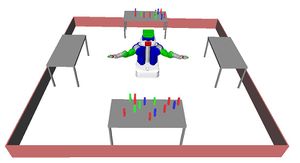
Problem 1 : Tower of Hanoi
Description
Tower of Hanoi with mobile robots[1].
Challenge
For n discs, 2n - 1 moves are needed (in the non-geometric case).
Placing a disk on the central rod may prevent, depending on their relative sizes, to transfer discs from rod 1 to rod 3 (or vice versa).
The problem has been adapted to a humanoid robot setup. The idea is to have similar geometric constraints by setting the positions of the rods in a triangular shape and by using "thick" discs, in order to cause collisions between forearms and discs.
Download
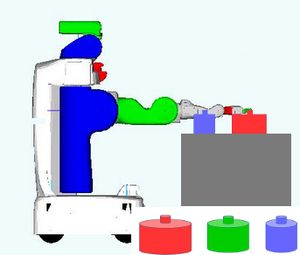
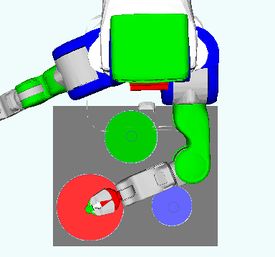
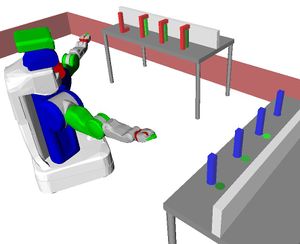
Problem 2 : Blocks-World 3D
Description
Using top-grasps only, and not using hand-over, stack the blocks in alphabetical order anywhere (on the table, or on one of the trays).
With a PR2 robot, the flying obstacle would be lower.
Challenge
Because of the "hovering obstacle", the pile cannot be built on the table.
Because of the "hovering obstacle", no more than 2 blocks can be stacked on the table (then the wrist touches the obstacle).
Whether the red or blue tray is chosen as location for building the pile, both initial piles need to be unstacked somewhere, somewhere reachable by both arms: R.
R is limited in size, and no more than 2 blocks can be stacked in this region, so there is a trade-off between:
- a short symbolic plan with a cluttered R
- a long symbolic plan with manageable R
Here is an example of solution.
Download
Problem 3 : Sorting Objects
Description
The goal constraints are that all 7 blue blocks must be on the left table and all 7 green blocks must be on the right table. There are also 14 red blocks.
Challenge
The close proximity of the blocks forces the planner to carefully order its operations as well as to move red blocks out of the way.
Download
Problem 4 : Non-Monotonic
Description
The robot must move the green blocks from the left table to a corresponding position on the right table. Both the initial and goal poses are blocked by four blue and cyan blocks respectively (blocking objects). In the goal state, blue and cyan blocks have to be in their initial poses.
Challenge
The goal condition of blue and cyan blocks requires to temporarily move them away and bring them back later on (non-monotonicity) in order to solve the problem.
Download
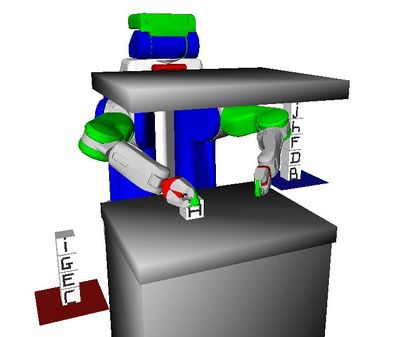
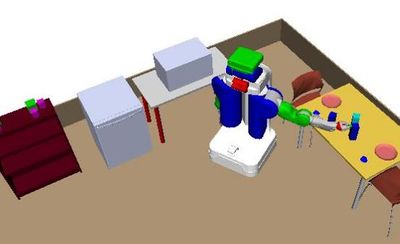
Problem 5 : Kitchen
Description
The robot must prepare a meal by cleaning two glasses (blue blocks), cooking two cabbages (green blocks), and setting the table. Objects can be cleaned when placed on the dishwasher and cooked when placed on the microwave. An object must be cleaned before it can be cooked. Finally, the radishes (pink blocks) initially obstruct the cabbages on the shelf forcing the robot to move them. But, to maintain a tidy kitchen, the robot must also return them to their initial poses.
Challenge
This benchmark demonstrates that these challenges do appear in target applications. It combines several criteria including blocking objects, non-monotonicity, and non-geometric actions (cleaning and cooking).
Download
Problem 6 : Rearrangement Planning (replaced by problem 3)
Description
The goal is to exchange the positions (i.e., the centre of objects) of the red object and the tray.
Challenge
One of the two objects has to be moved first to a temporary location. This may require to move other objects around, carefully choosing places that do not interfere.
The rearrangement planning problem [2] [3].
References
- ↑ S. Cambon, R. Alami, and F. Gravot. A hybrid approach to intricate motion, manipulation and task planning. The Int. Journal of Robotics Research, 2009.
- ↑ G. Havur et al., Geometric rearrangement of multiple movable objects on cluttered surfaces: A hybrid reasoning approach, Proceedings of ICRA 2014.
- ↑ F. Lagriffoul, B. Andres, Combining Task and Motion Planning: a culprit detection problem, The International Journal of Robotics Research, 2016.