Download page pb1

This page should contain all the necessary files/information to set this benchmark up. Until we agree on it, some of the input data is given as plain text.

Overview

Figure 1

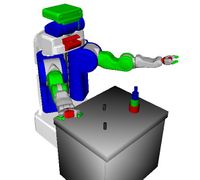
The main difference with the classic Tower of Hanoi problem is the disposition of the rods, which are not aligned, but set in a triangular fashion (the exact disposition may change later):

    2
3      1

Figure 2

Geometries

This archive file contains all the meshes in OBJ format (and .mtl files for colors):

hanoi_meshes.tar.gz

It includes:

• the rod
• the five discs
• the table

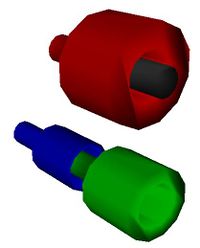
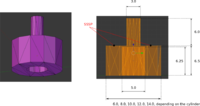
The "discs" are designed so that they can be stacked on each other without collision. The handle of the discs is 30mm in diameter. It is therefore easy to stack them since the hole under the discs is 50mm in diameter. The rod has the same dimensions than the handle (see Figures 2 and 3).

Figure 3

The origin of the reference frame attached to the object is located at the bottom, centre of the object. By bottom, we mean given that the object is standing in its "natural" upward orientation, if applicable. In this way, placing the object on a SSSP is achieved by placing the origin of its reference frame on the SSSP.

Initial poses

Waiting for a better solution (but after all it's not too bad):

• the transformation matrices of all solids: pb1_3_discs.txt
• the initial configuration of PR2:

left_arm  ( 0.5, 0, 0, -0.16, 0, -0.11, 0)
right_arm (-0.5, 0, 0, -0.16, 0, -0.11, 0)
torso     ( 0.1 )

Movable objects

• disc1
• disc2
• disc3

Initial object attachments

(Although this is not relevant in this problem since one can only manipulate one disc at a time.)

• (table, disc3)
• (disc3, disc2)
• (disc2, disc1)

Surfaces supporting stable placements (SSSP)

• the table
• the top part of the disc3 (see Figure 3)
• the top part of the disc2

Stable object poses (SOP)

For disc1, disc2, disc3: any rotation of the initial pose about the world z-axis.

Other constraints

The base is not allowed to move in this problem.

Grasps

I think we should define a "side-grasp" template, which can be rotated about the world z-axis in order to generate all the possible grasps allowed for solving this problem.
See also Benchmarking suggestion 2 and Comment 5.

  TODO : 

Symbolic domain

hanoi.pddl

Problems

hanoi_pb_3.pddl
hanoi_pb_4.pddl
hanoi_pb_5.pddl
hanoi_pb_6.pddl

Wrapping everything in a single file

problem.xml