Difference between revisions of "Problems"
(→Description) |
(→Problem 5 : Kitchen) |
||
| (51 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
{| class="wikitable" style="text-align: center; | {| class="wikitable" style="text-align: center; | ||
|- | |- | ||
| − | ! Features !! Pb 1 !! Pb 2 !! Pb 3 !! Pb 4 !! Pb 5 !! Discussed in | + | ! Features !! Pb 1 !! Pb 2 !! Pb 3 !! Pb 4 !! Pb 5 !! Pb6 !!Discussed in |
|- | |- | ||
| − | | blocking objects || || || | + | | blocking objects || || || X || X || X || || [[Comments_from_Calean#Benchmarking_suggestion_3_17|bench. sugg. 3]] |
|- | |- | ||
| − | | large task spaces || X || X || || || || [[Comments_from_Calean#Benchmarking_suggestion_3_17|bench. sugg. 3]], [[Comments_from_Neil#Difficult_problem_instances_10|diff. pb. inst.]] | + | | large task spaces || X || X || X || || || || [[Comments_from_Calean#Benchmarking_suggestion_3_17|bench. sugg. 3]], [[Comments_from_Neil#Difficult_problem_instances_10|diff. pb. inst.]] |
|- | |- | ||
| − | | | + | | infeasible task operators || x || X || || || || || [[Comments_from_Calean#Benchmarking_suggestion_3_17|bench. sugg. 3]], [[Comments_from_Neil#Difficult_problem_instances_10|diff. pb. inst.]] |
|- | |- | ||
| − | | | + | | trade-off motion planning/task planning || || X || || || || || [[Talk:Problems#Difficult_problem_instances_10|diff. pb. inst.]] |
|- | |- | ||
| − | | | + | | non-monotonicity || || || || X || X || X || [[Talk:Problems#Benchmarking_suggestion_4_27|bench. sugg. 4]] |
|- | |- | ||
| − | | | + | | Non-geometric actions || || || || || X || || [[Talk:Problems#Comment_4_52|Sidd. comment 4]] |
|} | |} | ||
== Problem 1 : Tower of Hanoi == | == Problem 1 : Tower of Hanoi == | ||
| − | [[File:bm1.jpg|problem 1|300px]] | + | [[File:bm1.jpg|problem 1|300px]] [[File:hanoi1.jpg|problem 1|300px]] [[File:hanoi2.jpg|problem 1|275px]] |
==== Description ==== | ==== Description ==== | ||
| − | Tower of Hanoi | + | This is the classical Tower of Hanoi problem (inspired by Cambon et al.<ref>S. Cambon, R. Alami, and F. Gravot. A hybrid approach to intricate motion, manipulation and task planning. The Int. Journal of Robotics Research, 2009.</ref>.). The base of the robot is fixed. The rods are set in a triangular fashion and the discs are very thick, so that stacking them on a rod may temporarily create an obstacle and prevent from picking/placing discs on other rods. |
==== Challenge ==== | ==== Challenge ==== | ||
| − | + | Although the rules are simple, the optimal solution plan for ''n'' discs contains ''2''<sup>''n''</sup> - ''1'' steps, without con- | |
| − | + | sidering geometry (large task space). The rules of the game impose to go through intermediate states, many of which are geometrically unfeasible (unfeasible task operators) if the chosen order creates occlusions. | |
| + | |||
| + | ==== Download ==== | ||
| + | [[download_page_pb1|Download page (PR2)]] | ||
== Problem 2 : Blocks-World 3D == | == Problem 2 : Blocks-World 3D == | ||
| − | [[File:bm2.jpg|problem 2| | + | [[File:bm2-pr2.jpg|problem 2|400px]] |
==== Description ==== | ==== Description ==== | ||
| − | + | Another classical task planning problem, in which the goal is to stack the blocks in alphabetical order anywhere it is possible. The base is fixed, only top-grasps can be used, and hand-over is not allowed. An obstacle is hovering over the table, such that the grippers would collide with it if more than 2 blocks are stacked on the table (unfeasible task operators). | |
| − | |||
==== Challenge ==== | ==== Challenge ==== | ||
| − | + | Both initial piles need to be un-stacked somewhere and re-stacked on one of the trays. During this process, half of the blocks need to transit from one tray to another, through the table. This requires many actions (large task space). The region on the table where blocks transit has to be reachable by both arms, therefore its size is limited. One must choose between few steps and cluttered table, or many steps and uncluttered table (motion/task trade-off). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == Problem 3 : | + | ==== Download ==== |
| − | [[File: | + | [[download_page_pb2|Download page (PR2)]] |
| + | |||
| + | == Problem 3 : Sorting Objects == | ||
| + | [[File:bm4.jpg|problem 4|400px]] | ||
==== Description ==== | ==== Description ==== | ||
| + | The goal constraints are that all N blue blocks must be on the left table and all N green blocks must be on the right table. There are also 2N red blocks acting as obstacles for reaching blue and green blocks. | ||
| + | |||
| + | ==== Challenge ==== | ||
| + | The close proximity of the blocks forces the planner to carefully order its operations, as well as to move red blocks out of the way without creating new occlusions (blocking objects). Solving the problem requires to move many objects, sometimes multiple times (large task space). | ||
| + | |||
| + | ==== Download ==== | ||
| + | [[download_page_pb3|Download page (PR2)]] | ||
| + | |||
| + | == Problem 4 : Non-Monotonic == | ||
| + | [[File:Bm5.jpg|problem 5|300px]] | ||
| − | The | + | ==== Description ==== |
| + | The robot must move the green blocks from the left table to a corresponding position on the right table. Both the initial and goal poses are blocked by four red and blue blocks respectively. In the goal state, red and blue blocks have to be at their respective initial locations. | ||
==== Challenge ==== | ==== Challenge ==== | ||
| − | + | The goal condition of blue and cyan blocks requires to temporarily move them away and bring them back later on (non-monotonicity) in order to solve the problem. | |
| − | |||
| − | + | ==== Download ==== | |
| − | + | [[download_page_pb4|Download page (PR2)]] | |
| − | |||
| − | == Problem | + | == Problem 5 : Kitchen == |
| − | [[File: | + | [[File:Kitchen.png|problem 5|350px]] |
==== Description ==== | ==== Description ==== | ||
| − | The | + | The robot must prepare a meal by cleaning two glasses (blue cylinders), cooking two cabbages (green blocks), and setting the table. Objects can be cleaned when placed on the dishwasher and cooked when placed on the microwave. An object must be cleaned before it can be cooked. Finally, the radishes (pink blocks) initially obstruct the cabbages on the shelf forcing the robot to move them. But, to maintain a tidy kitchen, the robot must also return them to their initial poses (the tray). |
==== Challenge ==== | ==== Challenge ==== | ||
| − | + | This benchmark demonstrates that these challenges do appear in target applications. It combines several criteria including blocking objects, non-monotonicity, and non-geometric actions (cleaning and cooking). | |
| + | |||
| + | ==== Download ==== | ||
| + | [[download_page_pb5|Download page (PR2)]] | ||
| − | == Problem | + | == Problem 6 : '''(DEPRECATED)''' Rearrangement Planning (replaced by problem 4) == |
| − | [[File: | + | [[File:bm3.jpg|problem 3|400px]] |
==== Description ==== | ==== Description ==== | ||
| − | The | + | |
| + | The goal is to exchange the positions (i.e., the centre of objects) of the red object and the tray. | ||
==== Challenge ==== | ==== Challenge ==== | ||
| − | + | One of the two objects has to be moved first to a temporary location. | |
| + | This may require to move other objects around, carefully choosing places that do not interfere. | ||
| + | |||
| + | The rearrangement planning problem | ||
| + | <ref>G. Havur et al., ''Geometric rearrangement of multiple movable objects on cluttered surfaces: A hybrid reasoning approach'', Proceedings of ICRA 2014.</ref> | ||
| + | <ref>F. Lagriffoul, B. Andres, ''Combining Task and Motion Planning: a culprit detection problem'', The International Journal of Robotics Research, 2016.</ref>. | ||
== References == | == References == | ||
Latest revision as of 15:45, 27 May 2018
Table summarizing some features we want to test. To be refined or extended.
| Features | Pb 1 | Pb 2 | Pb 3 | Pb 4 | Pb 5 | Pb6 | Discussed in |
|---|---|---|---|---|---|---|---|
| blocking objects | X | X | X | bench. sugg. 3 | |||
| large task spaces | X | X | X | bench. sugg. 3, diff. pb. inst. | |||
| infeasible task operators | x | X | bench. sugg. 3, diff. pb. inst. | ||||
| trade-off motion planning/task planning | X | diff. pb. inst. | |||||
| non-monotonicity | X | X | X | bench. sugg. 4 | |||
| Non-geometric actions | X | Sidd. comment 4 |
Contents
Problem 1 : Tower of Hanoi
Description
This is the classical Tower of Hanoi problem (inspired by Cambon et al.[1].). The base of the robot is fixed. The rods are set in a triangular fashion and the discs are very thick, so that stacking them on a rod may temporarily create an obstacle and prevent from picking/placing discs on other rods.
Challenge
Although the rules are simple, the optimal solution plan for n discs contains 2n - 1 steps, without con- sidering geometry (large task space). The rules of the game impose to go through intermediate states, many of which are geometrically unfeasible (unfeasible task operators) if the chosen order creates occlusions.
Download
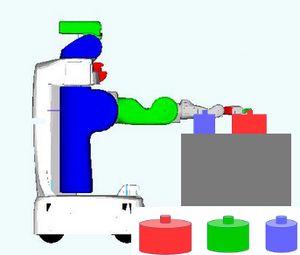
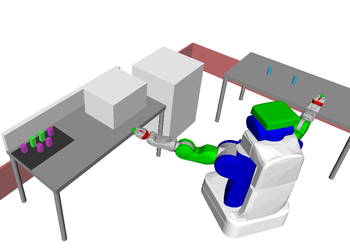
Problem 2 : Blocks-World 3D
Description
Another classical task planning problem, in which the goal is to stack the blocks in alphabetical order anywhere it is possible. The base is fixed, only top-grasps can be used, and hand-over is not allowed. An obstacle is hovering over the table, such that the grippers would collide with it if more than 2 blocks are stacked on the table (unfeasible task operators).
Challenge
Both initial piles need to be un-stacked somewhere and re-stacked on one of the trays. During this process, half of the blocks need to transit from one tray to another, through the table. This requires many actions (large task space). The region on the table where blocks transit has to be reachable by both arms, therefore its size is limited. One must choose between few steps and cluttered table, or many steps and uncluttered table (motion/task trade-off).
Download
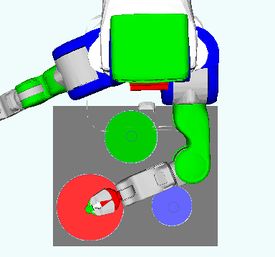
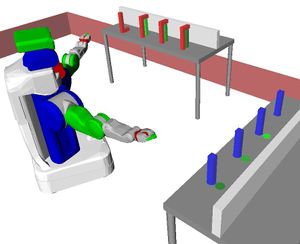
Problem 3 : Sorting Objects
Description
The goal constraints are that all N blue blocks must be on the left table and all N green blocks must be on the right table. There are also 2N red blocks acting as obstacles for reaching blue and green blocks.
Challenge
The close proximity of the blocks forces the planner to carefully order its operations, as well as to move red blocks out of the way without creating new occlusions (blocking objects). Solving the problem requires to move many objects, sometimes multiple times (large task space).
Download
Problem 4 : Non-Monotonic
Description
The robot must move the green blocks from the left table to a corresponding position on the right table. Both the initial and goal poses are blocked by four red and blue blocks respectively. In the goal state, red and blue blocks have to be at their respective initial locations.
Challenge
The goal condition of blue and cyan blocks requires to temporarily move them away and bring them back later on (non-monotonicity) in order to solve the problem.
Download
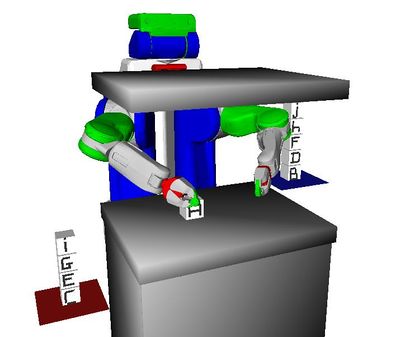
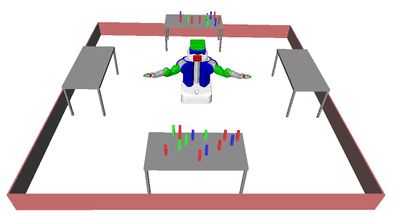
Problem 5 : Kitchen
Description
The robot must prepare a meal by cleaning two glasses (blue cylinders), cooking two cabbages (green blocks), and setting the table. Objects can be cleaned when placed on the dishwasher and cooked when placed on the microwave. An object must be cleaned before it can be cooked. Finally, the radishes (pink blocks) initially obstruct the cabbages on the shelf forcing the robot to move them. But, to maintain a tidy kitchen, the robot must also return them to their initial poses (the tray).
Challenge
This benchmark demonstrates that these challenges do appear in target applications. It combines several criteria including blocking objects, non-monotonicity, and non-geometric actions (cleaning and cooking).
Download
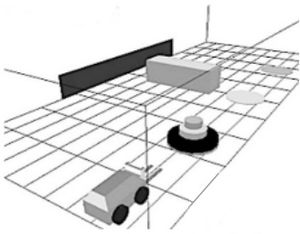
Problem 6 : (DEPRECATED) Rearrangement Planning (replaced by problem 4)
Description
The goal is to exchange the positions (i.e., the centre of objects) of the red object and the tray.
Challenge
One of the two objects has to be moved first to a temporary location. This may require to move other objects around, carefully choosing places that do not interfere.
The rearrangement planning problem [2] [3].
References
- ↑ S. Cambon, R. Alami, and F. Gravot. A hybrid approach to intricate motion, manipulation and task planning. The Int. Journal of Robotics Research, 2009.
- ↑ G. Havur et al., Geometric rearrangement of multiple movable objects on cluttered surfaces: A hybrid reasoning approach, Proceedings of ICRA 2014.
- ↑ F. Lagriffoul, B. Andres, Combining Task and Motion Planning: a culprit detection problem, The International Journal of Robotics Research, 2016.