Difference between revisions of "Problems"
(→Challenge) |
(→Problem 3 : Sorting Objects) |
||
| Line 62: | Line 62: | ||
==== Challenge ==== | ==== Challenge ==== | ||
The close proximity of the blocks forces the planner to carefully order its operations as well as to move red blocks out of the way. | The close proximity of the blocks forces the planner to carefully order its operations as well as to move red blocks out of the way. | ||
| + | |||
| + | ==== Download ==== | ||
| + | [[download_page_pb3|Download page]] | ||
== Problem 4 : Non-Monotonic == | == Problem 4 : Non-Monotonic == | ||
Revision as of 18:49, 24 February 2018
Table summarizing some features we want to test. To be refined or extended.
| Features | Pb 1 | Pb 2 | Pb 3 | Pb 4 | Pb 5 | Pb6 | Discussed in |
|---|---|---|---|---|---|---|---|
| blocking objects | X | X | bench. sugg. 3 | ||||
| large task spaces | X | X | bench. sugg. 3, diff. pb. inst. | ||||
| infeasible task operators | x | X | bench. sugg. 3, diff. pb. inst. | ||||
| trade-off motion planning/task planning | X | diff. pb. inst. | |||||
| non-monotonicity | X | X | bench. sugg. 4 | ||||
| NAMO | ? | X | X | X | Sidd. comment 4 | ||
| Non-geometric actions | X | Sidd. comment 4 |
Contents
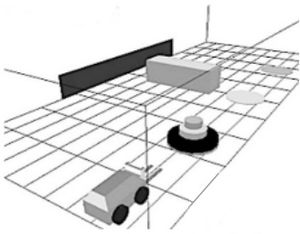
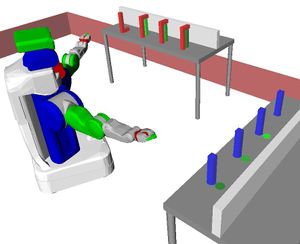
Problem 1 : Tower of Hanoi
Description
Tower of Hanoi with mobile robots[1].
Challenge
For n discs, 2n - 1 moves are needed (in the non-geometric case).
Placing a disk on the central rod may prevent, depending on their relative sizes, to transfer discs from rod 1 to rod 3 (or vice versa).
The problem has been adapted to a humanoid robot setup. The idea is to have similar geometric constraints by setting the positions of the rods in a triangular shape and by using "thick" discs, in order to cause collisions between forearms and discs.
Download
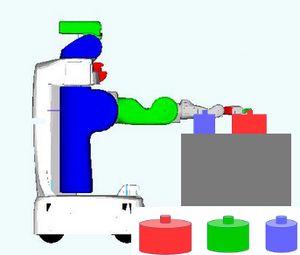
Problem 2 : Blocks-World 3D
Description
Using top-grasps only, and not using hand-over, stack the blocks in alphabetical order anywhere (on the table, or on one of the trays).
With a PR2 robot, the flying obstacle would be lower.
Challenge
Because of the "hovering obstacle", the pile cannot be built on the table.
Because of the "hovering obstacle", no more than 2 blocks can be stacked on the table (then the wrist touches the obstacle).
Whether the red or blue tray is chosen as location for building the pile, both initial piles need to be unstacked somewhere, somewhere reachable by both arms: R.
R is limited in size, and no more than 2 blocks can be stacked in this region, so there is a trade-off between:
- a short symbolic plan with a cluttered R
- a long symbolic plan with manageable R
Here is an example of solution.
Download
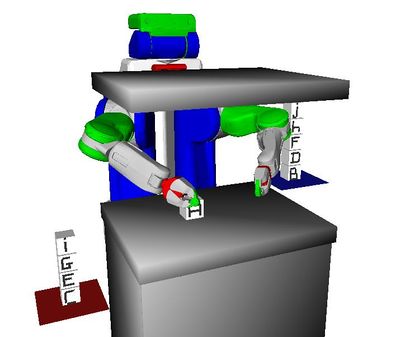
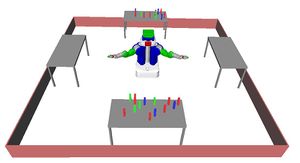
Problem 3 : Sorting Objects
Description
The goal constraints are that all 7 blue blocks must be on the left table and all 7 green blocks must be on the right table. There are also 14 red blocks.
Challenge
The close proximity of the blocks forces the planner to carefully order its operations as well as to move red blocks out of the way.
Download
Problem 4 : Non-Monotonic
Description
The robot must move the green blocks from the left table to a corresponding position on the right table. Both the initial and goal poses are blocked by four blue and cyan blocks respectively.
Challenge
Critically, the blue and cyan blocks have goal conditions to remain in their initial poses. This is the source of the nonmonotonicity as the robot must undo several goals by moving the blue and cyan blocks in order to solve the problem.
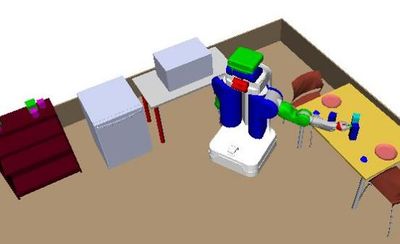
Problem 5 : Kitchen
Description
The robot must obtain two green cabbages from the shelves, clean them on the dishwasher, cook them on the microwave, and serve them. Additionally, the robot must organize the dirty cups on the table, clean them, and set the table.
Challenge
TODO
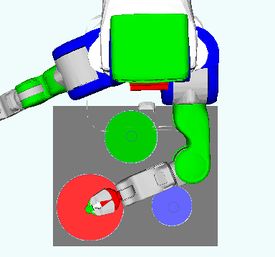
Problem 6 : Rearrangement Planning (replaced by problem 3)
Description
The goal is to exchange the positions (i.e., the centre of objects) of the red object and the tray.
Challenge
One of the two objects has to be moved first to a temporary location. This may require to move other objects around, carefully choosing places that do not interfere.
The rearrangement planning problem [2] [3].
References
- ↑ S. Cambon, R. Alami, and F. Gravot. A hybrid approach to intricate motion, manipulation and task planning. The Int. Journal of Robotics Research, 2009.
- ↑ G. Havur et al., Geometric rearrangement of multiple movable objects on cluttered surfaces: A hybrid reasoning approach, Proceedings of ICRA 2014.
- ↑ F. Lagriffoul, B. Andres, Combining Task and Motion Planning: a culprit detection problem, The International Journal of Robotics Research, 2016.